مسألة 8: رسم قاطع لدائرتين متحدين بالمركز

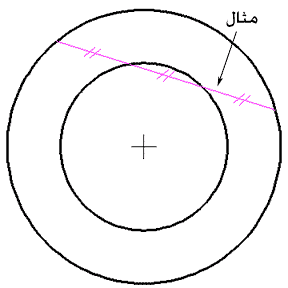
الحل:

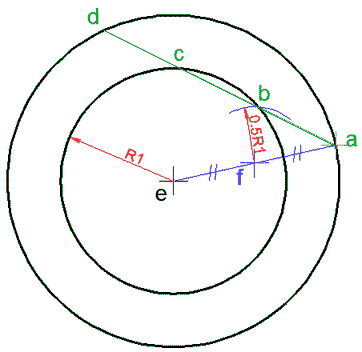
 نختار نقطة a من محيط الدائرة الكبيرة.

نعين النقطة f منتصف ae حيث e هو المركز المشترك للدائرتين.

نرسم قوساً مركزه f ونصف قطره هو نصف نصف قطر الدائرة الصغرى، أي قطره يساوي نصف قطر الدائرة الصغرى، فتكون نقطة تقاطعها مع الدائرة الصغرى هي b.

نصل ab ونمده فيقطع الدائرة الصغيرة مرة أخرى في c ويقطع الكبيرة في d، وتكون القطعة المطلوبة هي ad.

نلاحظ أنه حتى يوجد حل يجب أن يكون R2<3R1 حيث R2 هو نصف قطر الدائرة الكبيرة.

البرهان:

يكفي أن نثبت أن ab = bc، لأن ab = cd دائماً مهما كان الوتر.

المثلثان abf و ace متشابهان، لأن الزاوية a مشتركة، ونسبة af/ae تساوي النسبة bf/ce وتساوي 1/2، إذن ab/ac =1/2 مما يعني أن ab = bc