مسألة 6: رسم مثلث متساوي الأضلاع على مستقيمين ونقطة
تم نشر هذه المسألة في ملتقى المهندسين العرب على الرابط:
www.arab-eng.org/vb/t206066.html
نص المسألة:
لدينا مستقيمان xy و yz متقاطعان في y وبينهما زاوية α، وa نقطة من مستويهما، والمطلوب رسم مثلث متساوي الأضلاع أحد رؤوسه a والرأسان الآخران يقعان على المستقيمين السابقين كما في الشكل:
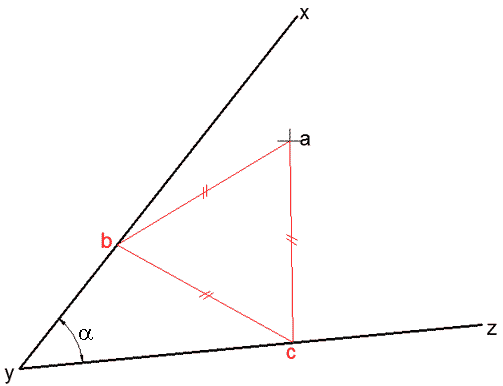
توجد حالة خاصة لقيمة الزاوية α لا يمكن عندها رسم هذا المثلث، ما قياس هذه الزاوية؟
الحل:
نرسم من a عموداً على xy فيقطعه في d. (راجع الأساسيات)
نرسم مثلثاً aed متساوي الأضلاع أحد أضلاعه da بأن نفتح الفرجار بفتحة da ونركزه في a ونرسم قوساً، ثم نركزه في d ونرسم قوساً يتقاطع مع السابق في e.
نرسم عموداً على ea ماراً من e فيتقاطع مع yz في c
نفتح الفرجار بقيمة ac ونركزه في a ونرسم قوساً يتقاطع مع xy في b
المثلث المطلوب هو abc.
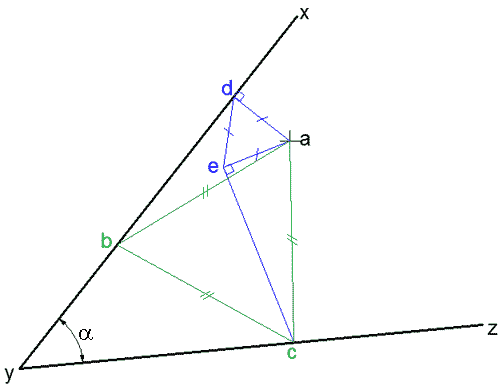
البرهان:
المثلثان aec و adb متطابقان لأن فيهما زاوية قائمة وضلعان متساويان وهما ad=ae و ab=ac.
أي الزاويتان التاليتان متساويتان: dab=eac
نطرح من كل منهما الزاوية eab فنجد أن bac=dae=60 فالمثلث abc متساوي الأضلاع لأنه متساوي الساقين وفيه زاوية 60.
بناءً على الحل السابق فإنه إذا كان ec يوازي yz فإنهما لن يتقاطعا والزاوية α عندها تساوي 120 درجة، أي تساوي الزاوية بين ec و xy
ملاحظة: هناك حلان للمسألة في الحالة العامة، الحل الأول كما تم رسمه،
والثاني عندما تكون e في الجهة المقابلة بالنسبة ل da ولهذا الحل زاوية
أخرى α لا تحقق المطلوب.

هاتف: +963-31-2220008
جوال: +963-999-824193
سوريا - حمص