مسألة 7: رسم مثلث متساوي الأضلاع على ثلاثة دوائر متحدة المركز

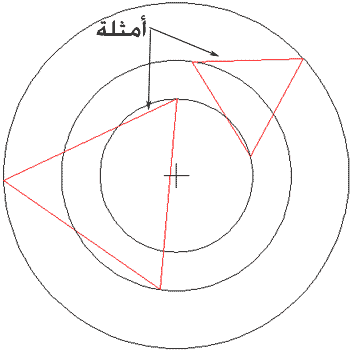
الحل:

بفرض الدائرة الصغيرة رقمها 1 والوسطى 2 والكبيرة 3. أنصاف أقطارها R1 و R2 و R3 على التوالي. المركز المشترك هو d.

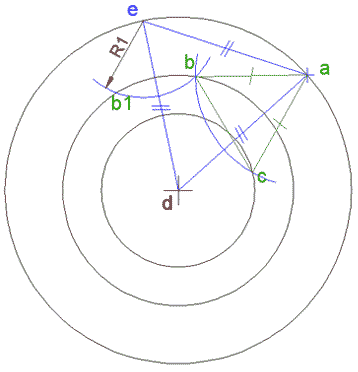
نختار نقطة a من الدائرة 3 (وهي الرأس الأول) ثم نركز الفرجار في a وبفتحة R3 نرسم قوساً يقطع الدائرة 3 في e، فيكون المثلث dae متساوي الأضلاع.

نركز الفرجار في e وبفتحة R1 (نصف قطر الدائرة 1) نرسم قوساً يقطع الدائرة 2 في b و b1.

النقطة b هي الرأس الثاني للمثلث الأول، و b1 هي الرأس الثاني للمثلث الثاني (لم يتم رسمه لتوضيح الرسم)

نركز الفرجار في a وبفتحة تساوي ba (أو b1a) نرسم قوساً يقطع الدائرة 1 في c (أو c1) هي الرأس الثالث.

المثلث المطلوب هو abc أو ab1c1

البرهان:

abc مثلث متساوي الساقين لأن ab=ac وذلك من الخطوة الأخيرة.

يكفي أن نبرهب أن الزاوية bac=60 ليكون المثلث متساوي الأضلاع.

المثلثين abe و acd متطابقين لتساوي كل ضلعين متقابلين، إذن الزاويتين cad و bae متساويتين.

نضيف لكل منهما الزاوية dab فيكون:

cad+dab=bae+dab

وبما أن bae+dab=dae=60 إذن cad+dab=bac=60 وهو المطلوب.