مسألة 5: رسم قطعة مستقيمة على دائرتين متقاطعتين

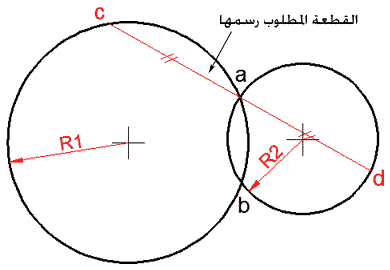
الحل:

أيضاً لهذه المسألة عدة حلول، وقد اخترت أحدها.

نصل a بمركز الدائرة الأولى ونمده من جهة a بطول R1 (نصف قطر الدائرة الأولى) فنحصل على e

نفتح الفرجار بفتحة R1 ونركزه في e ونرسم قوساً يتقاطع مع الدائرة الثانية في d

نصل da ونمده حتى يقطع الدائرة الأولى في c

فتكون cd هي القطعة المطلوبة.

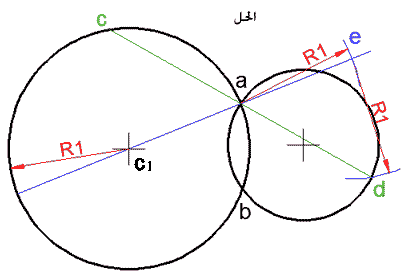
البرهان:

المثلثان ead و c₁ac مثلثان متطابقان بسبب أن كليهما متساوي الساقين (طول الضلع R1) والزاوية a من الأول تساوي الزاوية a من الثاني بسبب التقابل بالرأس فهما حتى الآن متشابهان، وبما أن ea = c₁a فهما متطابقين، إذن ad = ac.