أساسيات في الإنشاء أو الرسم الهندسي
تم طرح هذا الموضوع أولاً في ملتقى المهندسين العرب على هذا الرابط:
http://www.arab-eng.org/vb/t204401.html
مقدمة:
أتكلم في هذا الموضوع عن بعض طرق الرسم الإنشائي البسيطة، والتي تعتبر نواةً للرسوم الإنشائية الأعقد.
من هذه الرسوم مثلاً رسم منصف لزاوية، فإذا احتجنا في حل أحد التمارين إلى تنصيف زاوية abc، قلنا نرسم منصف الزاوية abc ولا داعي لشرح الطريقة لأنها من الأساسيات التي يفترض أنها معروفة.
لن أقوم ببرهان صحة هذه الأساسيات لأنها من البديهيات عند طالب الهندسة، وهي تستند إلى نظريات الهندسية المستوية، ويمكن إثباتها بسهولة.
أما الأدوات التي نستخدمها أثناء الإنشاء الهندسي فهي: مسطرة غير مرقمة – فرجار (بيكار) – قلم – مثلث قائم لرسم زاوية قائمة (ولكنه –أي المثلث- غير ضروري لأننا سنرى كيف نرسم زاوية قائمة باستخدام الفرجار والمسطرة)
أي لا يسمح باستخدام الآلة الحاسبة أو حساب الأطوال عن طريق قوانين الهندسة التحليلية، فذلك فرع آخر من فروع الهندسة.
والآن إلى الشرح.
1- رسم قطعة مستقيمة معلومة الطول منطبقة على مستقيم معلوم:
لدينا المستقيم المعلوم V والطول المعلوم ab والنقطة c على المستقيم V، والمطلوب تحديد النقطة d على V بحيث يكون طول cd يساوي طول ab.
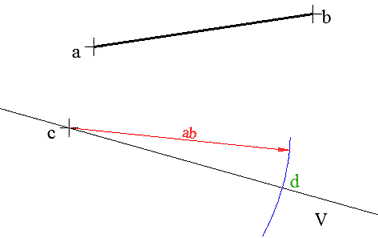
الحل:
نضع رأس الفرجار الأول في النقطة a ونفتحه لينطبق رأسه الثاني على b ونحافظ على الفتحة ونضع الرأس الأول في c ثم نرسم قوساً يقطع V في d وهي النقطة المطلوبة.
وإذا كان لدينا في نص المسألة الطول المعلوم عبارة عن رقم، فإنه في هذه الحالة يسمح باستخدام مسطرة مرقمة لفتح فتحة الفرجار الأولى بقيمة مساوية للطول المعلوم، ونتابع كما سبق.
2- رسم محور قطعة مستقيمة، ورسم دائرة تمر من رؤوس مثلث مفروض:
تعريف: محور قطعة مستقيمة هو المحل الهندسي للنقاط المتساوية البعد عن طرفي هذه القطعة، أي هو المحل الهندسي لمراكز الدوائر التي تمر من طرفي هذه القطعة.
لدينا القطعة المستقيمة المعلومة ab والمطلوب رسم محور هذه القطعة، أي رسم مستقيم عمودي على هذه القطعة في منتصفها.
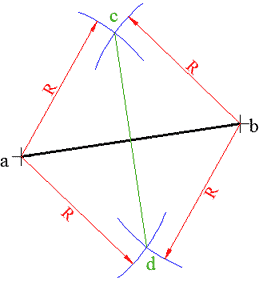
الحل:
نفتح فتحة الفرجار فتحة عشوائية R بحيث تكون أكبر من نصف طول القطعة ab ثم نثبت رأس الفرجار في a ونرسم قوسي دائرة على جانبي القطعة ab كما في الشكل، ثم نثبت رأس الفرجار في b مع المحافظة على نفس الفتحة ونرسم أيضاً قوسين يتقاطعان مع السابقين في c و d.
نصل cd فنحصل على المحور المطلوب.
نستفيد من رسم المحور في تحديد منتصف قطعة مستقيمة وفي تحديد منحى عمودي عليها.
ولرسم دائرة تمر من رؤوس مثلث مفروض يكفي إنشاء محورين لضلعين من المثلث فتكون نقطة تلاقي هذين المحورين هي مركز الدائرة، ونصف قطرها هو المسافة بين هذا المركز وأحد رؤوس المثلث.
فائدة: لرسم دائرة يكفي تعيين مركزها ونقطة على محيطها، أو تعيين ثلاث نقاط من محيطها.
3- رسم عمود على قطعة مستقيمة من نقطة عليها أو خارجها:
لدينا القطعة المستقيمة ab والنقطة c والمطلوب رسم عمود من c على ab.
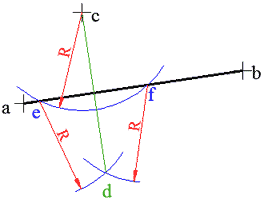
الحل:
نفتح الفرجار بفتحة عشوائية بحيث تكون أكبر من المسافة بين c و ab، نثبت رأسه في c ونرسم قوساً يتقاطع مع ab في e و f، ثم نثبت رأس الفرجار في e ونرسم قوساً في الجهة المقابلة لجهة c بالنسبة ل ab، ثم نثبت الفرجار في f مع المحافظة على نفس فتحته عندما ثبتناه في e ونرسم قوساً يتقاطع مع السابق في d.
نصل cd فنحصل على العمود المطلوب كما في الشكل.
4- تحديد مركز دائرة معلومة:
لتكن لدينا الدائرة المعلومة C والمطوب تحديد مركزها.
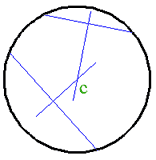
الحل:
نرسم وترين غير متوازيين لهذه الدائرة، ونرسم محوري هذين الوترين كما في البند 2 سابقاً، فتكون نقطة تقاطع هذين المحورين هي مركز الدائرة.
5- رسم مماس لدائرة معلومة من نقطة معلومة:
لدينا الدائرة المعلومة C والنقطة a تقع خارجها، والمطلوب رسم مماس لهذه الدائرة مار من a.
الحل:
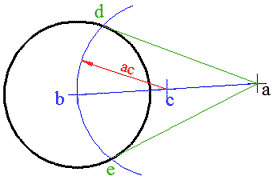
نحدد مركز الدائرة كما في البند 4 وسنسميه b، ثم نحدد منتصف القطعة ab كما في البند 2 ولتكن نقطة المنتصف اسمها c، نثبت الفرجار في c ونفتح فتحة تساوي ac ونرسم قوساً يتقاطع مع الدائرة C في نقطتين هما d و e، نصل a بهاتين النقطتين فنحصل على مماسين للدائرة C مارين من a هما ad و ae.
توضيح: المماس لدائرة في نقطة d يكون عمودياً على نصف قطر الدائرة المار من هذه النقطة d، أي أنه في الرسم أعلاه ad عمودي على bd، لذلك قمنا برسم دائرة أخرى مركزها c والوتران ad و bd فيها يحصران نصف دائرة، فتكون الزاوية بينهما زاوية قائمة.
6- تنصيف زاوية معلومة، ورسم دائرة تمس أضلاع مثلث مفروض:
لدينا الزاوية المعلومة (أي المرسومة) abc والمطلوب رسم منصفها.
الحل:
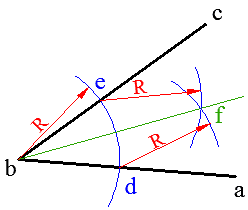
نفتح الفرجار بفتحة عشوائية ونثبته في b ونرسم قوساً يتقاطع مع ضلعي الزاوية في d و e.
نثبت الفرجار في d ونرسم قوساً، ثم نثبته في e مع المحافظة على نفس فتحته عندما ثبتناه في d ونرسم قوساً يتقاطع مع السابق في f، نصل bf فيكون هو المنصف المطلوب.
فائدة: المحل الهندسي لمراكز الدوائر المماسة لضلعي زاوية هو منصف هذه الزاوية.
لذلك لرسم دائرة تمس أضلاع مثلث يكفي رسم منصفي زاويتين من زوايا المثلث فتكون نقطة تقاطع هذين المنصفين هي مركز الدائرة، ولتحديد نقطة من محيط الدائرة ننزل عموداً من المركز على أحد الأضلاع كما في البند 3، فتكون نقطة تقاطع هذا العمود مع الضلع هي نقطة من محيط الدائرة.
7- رسم زاوية مطابقة لزاوية معلومة:
لدينا الزاوية المعلومة abc ولدينا القطعة المستقيمة de والمطلوب رسم زاوية أحد أضلاعها de ورأسها هو e وتساوي الزاوية abc.
الحل:
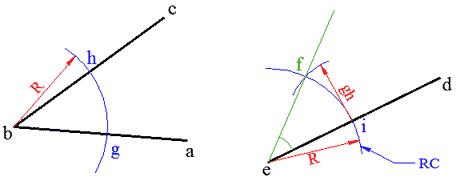
نفتح الفرجار فتحة عشوائية R ونثبته في b ونرسم قوساً يتقاطع مع ضلعي الزاوية abc في g و h.
مع المحافظة على نفس فتحة الفرجار نثبته في e ونرسم قوساً سنسميه RC يتقاطع مع de في i.
نفتح الفرجار بفتحة تساوي gh ونثبته في i ونرسم قوساً يتقاطع مع القوس RC في f.
نصل ef فنحصل على الزاوية المطلوبة وهي def.
8- رسم مستقيم مار من نقطة معلومة ويوازي مستقيماً معلوماً:
لدينا مستقيم V ونقطة معلومة a لا تقع عليه، والمطلوب رسم مستقيم يوازي V ويمر من a.
الحل:
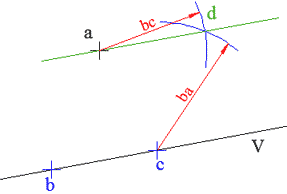
نحدد نقطتين b و c على V بشكل عشوائي، نثبت الفرجار في b ونفتحه بفتحة تساوي المسافة ba ثم نثبته في c مع المحافظة على الفتحة ونرسم قوساً.
نثبت الفرجار في b ونفتحة بفتحة تساوي المسافة bc ثم نثبته في a مع المحافظة على الفتحة ونرسم قوساً يتقاطع مع السابق في d.
المستقيم المطلوب هو ad.
9- رسم مثلث متساوي الأضلاع، ومنه نستنتج طريقة رسم الزاوية 60 درجة:
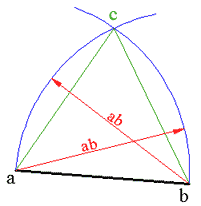
لدينا قطعة مستقيمة معلومة ab والمطلوب رسم مثلث متساوي الأضلاع أحد أضلاعه هو ab.
الحل:
نثبت الفرجار في a ونفتحه بفتحة تساوي ab ثم نرسم قوساً.
نثبت الفرجار في b مع المحافظة على نفس المسافة ونرسم قوساً يتقاطع مع السابق في c هي الرأس الثالث للمثلث.
لاحظ وجود حلين للمسألة.
إذاً لرسم زاوية 60 درجة يكفي رسم مثلث متساوي الأضلاع.
10- طريقة رسم الزاوية 30 درجة:
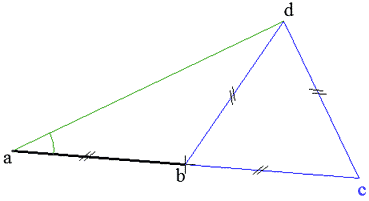
لدينا القطعة المستقيمة ab والمطلوب رسم زاوية قيمتها 30 درجة أحد أضلاعها ab ورأسها a.
الحل:
نمد القطعة ab من جهة b بطول يساوي ab باستخدام المسطرة والفرجار فنحصل على نقطة c.
نرسم مثلثاً متساوي الأضلاع أحد أضلاعه bc كما في البند 9 أعلاه، فيكون رأسه الثالث d.
نصل ad فنحصل على زاوية هي dab قياسها 30 درجة.
11- تقسيم قطعة مستقيمة داخلياً بنسبة محددة:
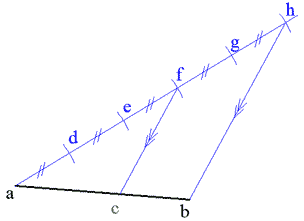
لدينا القطعة المستقيمة ab والمطلوب تحديد نقطة c بحيث تقسم تلك القطعة المستقيمة داخلياً بنسبة 3 إلى 2 أي يكون:
ca/cb=3/2 , or ca/ab=3/5
الحل:
من النقطة a نرسم مستقيماً يصنع مع ab زاوية لا على التعيين، ثم نحدد عليه نقطة d أيضاً لا على التعيين.
نفتح الفرجار بفتحة تساوي ad ونركزه في d ونرسم قوساً يقطع المستقيم السابق في e.
نعيد العملية ونركز الفرجار في e ونرسم قوساً يقطع المستقيم السابق في f.
نكرر العملية لنحصل على g و h. وهكذا حصلنا على قطعة مستقيمة ah مقسمة إلى 5 قطع متساوية.
نصل hb ثم نرسم من f موازياً ل hb يقطع ab في c هي النقطة المطلوبة.
هذه أهم طرق الإنشاء الهندسي الأساسية التي خطرت في بالي، وللاطلاع على المسائل يمكنكم استخدام القائمة الجانبية.

هاتف: +963-31-2220008
جوال: +963-999-824193
سوريا - حمص