تطبيقات برمجة أوتوكاد - التطبيق الأول - نجوم أوتوكاد

تم نشر هذا التطبيق في قسم المقالات في موقع CadMagazine عام 2001 بعنوان نجوم أوتوكاد، وكان رقم إصدار أوتوكاد وقتها 2000، وسأقوم بنقل هذا التمرين هنا كما هو.

المستوى

متوسط

مقدمة

بسم الله الرحمن الرحيم، والصلاة والسلام على سيدنا محمد، وعلى آله وأصحابه أجمعين...

أتحدث في هذه المقالة عن رسم الأشكال النجمية المنتظمة في أوتوكاد باستخدام لغة البرمجة فيجوال بيسك للتطبيقات (VBA)، المتوفرة أصلاً في أوتوكاد. وللاستفادة من هذه المقالة يجب أن يكون القارئ على دراية سابقة بمبادئ فيجوال بيسك وأوتوكاد.

يعلم معظمكم أنه لا تتوفر في أوتوكاد أوامر جاهزة لرسم الأشكال النجمية، ولذلك فقد صممت برنامجاً ليقوم بهذه المهمة لهدفين، أولهما: إطلاع القارئ على طريقة استخدام لغة فيجوال بيسك للتطبيقات في أوتوكاد، وثانيهما: وضع هذا البرنامج في متناول مستخدمي برنامج أوتوكاد، مجاناً. وفي ما يلي بعض الأشكال النجمية التي يمكن الحصول عليها بسهولة باستخدامه.

الشكل (1): بعض الأشكال النجمية التي يمكن الحصول عليها.

الفكرة النظرية

نحتاج قبل البدء برسم النجم إلى معرفة المعطيات التالية، الموضحة في الشكل (2)

هذه المعطيات سيقوم المستخدم بإدخالها، وهي: مركز النجم c إحداثياه (x,y)، والعدد الكلي لرؤوس النجم، أو عدد الرؤوس الخارجية فقط، وسنستخدم هنا عدد الرؤوس الخارجية n، وهو نصف العدد الكلي للرؤوس، والقطر الكبير r1، والقطر الصغير r2.

سيتولى البرنامج مهمة حساب إحداثيات رؤوس النجم، ومن ثم يقوم برسم مجمع خطوط (polyline)، باستخدام تلك الإحداثيات المحسوبة.

طريقة الحساب

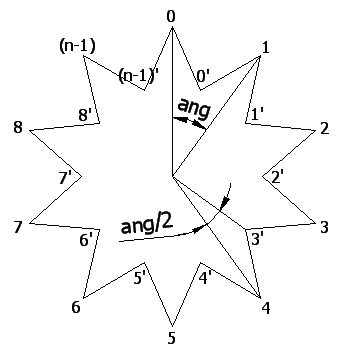
إن الزاوية ang الموضحة في الشكل (3)، هي ( ang = 2*pi / n )، حيث n: عدد الرؤوس الخارجية.

إن إحداثيات الرأس الخارجي i بالنسبة للمركز هي:

x(i) = r1 * sin(ang * i)
y(i) = r1 * cos(ang * i)

أما إحداثيات الرأس الداخلي i' بالنسبة للمركز فهي:

x’(i) = r2 * sin(ang * i + ang/2)
y’(i) = r2 * cos(ang * i + ang/2)

ومن الضروري أن ننتبه أن حساب تلك الإحداثيات بشكل عام يتطلب إضافة إحداثيات المركز لإحداثيات كل رأس، وهكذا تصبح المعادلات السابقة:

x(i) = r1 * sin(ang * i) + x
y(i) = r1 * cos(ang * i) + y

x’(i) = r2 * sin(ang * i + ang/2) + x
y’(i) = r2 * cos(ang * i + ang/2) + y

حيث x , y: إحداثيات المركز.

البدء بالبرنامج

لتشغيل بيئة VBA في أوتوكاد اضغط ALT + F11، فتظهر النافذة الرئيسية الموضحة في الشكل (4).

من قائمة "إدراج" (Insert) اختر "وحدة نمطية" (Module)، تظهر نافذة أخرى ضمن النافذة السابقة، سنقوم بكتابة البرنامج فيها.

نقوم بإضافة إجراء فرعي (Sub Procedure) ضمن النافذة، ونسميه DrawStar1، بكتابة السطر التالي:

Public Sub DrawStar1()

يقوم فيجوال بيسك للتطبيقات بإضافة السطر End Sub تلقائياً، ليصبح:

Public Sub DrawStar1()

End Sub

نضيف ما يلي بين السطرين السابقين:

Dim pnt1 As Variant, p(0 To 2) As Double
Dim n As Integer, r1 As Single, r2 As Single

حيث قمنا بتعريف مجموعة من المتحولات وهي:

pnt1: النقطة التي سنختارها ضمن نافذة أوتوكاد لتكون مركز النجم (متحول متغير يقبل جميع أنواع البيانات).
p (0 To 2): نفس النقطة ولكن بعد تحويلها إلى صيغة يقبلها أوتوكاد، لاحظ أن كل نقطة يتم تعريفها بشكل مصفوفة (Array) مؤلفة من ثلاثة عناصر هي إحداثيات هذه النقطة (أعداد حقيقية ذات دقة مضاعفة).
n: عدد الرؤوس الخارجية (عدد صحيح).
r1 و r2: أنصاف الأقطار (أعداد حقيقية ذات دقة مفردة).

أما الآن فسيطلب البرنامج من المستخدم إدخال مجموعة المعطيات باستخدام الأوامر التالية:

الوظيفة	الشرح
GetPoint	يطلب من المستخدم إدخال نقطة، إما بالنقر على موقع ما في إطار الرسم، أو بإدخال الإحداثيات في نافذة الأوامر
GetString	يطلب من المستخدم إدخال نص
GetReal	يطلب من المستخدم إدخال عدد حقيقي

وهذه الأوامر، بالإضافة إلى مجموعة من الأوامر الأخرى الشبيهة، هي من الطرق (methods) التابعة للكائن Utility، وهو كائن يمكن الوصول إليه من الكائن الأساسي ThisDrawing الذي يدل على ملف الرسم المفتوح حالياً. تستخدم هذه الأوامر بنفس الأسلوب.

أما الآن فسنتابع إدخال هذه الأوامر في البرنامج بعد السطرين السابقين، بحيث تبدو الشفرة النهائية لهذا الجزء كما يلي:

Public Sub DrawStar1()
    Dim pnt1 As Variant, p(0 To 2) As Double
    Dim n As Integer, r1 As Single, r2 As Single

    With ThisDrawing.Utility
        On Error GoTo anError
        pnt1 = .GetPoint(, "Specify center point: ")
        Do
            n1 = .GetString(0, "Enter number of outer vertices <8>: ")
            If n1 = "" Then n = 8 Else n = Val(n1)
            If n < 3 Then
                .Prompt "Value must be more than 2." & vbLf
            End If
        Loop While n < 3
        Do
            r1 = .GetReal("Specify first radius: ")
            If r1 <= 0 Then .Prompt "Value must be > 0"
        Loop Until r1 > 0
        Do
            r2 = .GetReal("Specify second radius: ")
            If r2 <= 0 Then .Prompt "Value must be > 0"
        Loop Until r2 > 0
    End With

    p(0) = pnt1(0): p(1) = pnt1(1): p(2) = pnt1(2)

    CalcStar p(), n, r1, r2
    Exit Sub
    anError:
End Sub

نلاحظ في السطر الرابع من الأسفل الأمر CalcStar، وهو في الحقيقة برنامج فرعي آخر يقوم بحساب إحداثيات الرؤوس ، وسنقوم بشرحه الآن.

أضف برنامجاً فرعياً بنفس الطريقة السابقة بأن تكتب في سطر فارغ ما يلي:

Private sub CalcStar (p() As Double, n As Integer, r1 As Single, r2 As Single)

يقوم فيجوال بيسك للتطبيقات بإضافة السطر End Sub تلقائياً.

سنقوم الآن بتعريف كائن جديد هو مجمع خطوط، كما يلي:

Dim lineObj As AcadPolyline

ثم نحسب الزاوية ang المشروحة سابقاً:

ang = 2 * pi / n

نقوم بحجز مصفوفة لتخزين إحداثيات رؤوس الشكل النجمي، وليكن اسمها Points، أما عدد عناصرها فهو ثلاثة أضعاف عدد النقاط الكلي، x و y و z لكل نقطة، وهذا العدد هو n1.

n1 = 3 * (2 * n) - 1
ReDim Points (0 to n1) As Double

ثم نقوم بحساب الإحداثيات وتخزينها ضمن المصفوفة Points، بالاعتماد على المعادلات السابقة:

For i = 0 To n - 1
    points(i * 6) = r1 * Sin(ang * i) + p(0)
    points(i * 6 + 1) = r1 * Cos(ang * i) + p(1)
    points(i * 6 + 2) = p(2)

    points(i * 6 + 3) = r2 * Sin(ang * i + ang / 2) + p(0)
    points(i * 6 + 4) = r2 * Cos(ang * i + ang / 2) + p(1)
    points(i * 6 + 5) = p(2)
Next

بقي لدينا الخطوة الأخيرة وهي رسم مجمع الخطوط بعد أن حسبنا إحداثيات رؤوس النجم، وسنستخدم لهذا الغرض الأمر AddPolyline، وهو واحد من الطرق (methods) التابعة لكائن حيز النموذج (ModelSpace) وهو بدوره تابع للكائن ThisDrawing.

Set lineObj = ThisDrawing.ModelSpace.AddPolyline(Points)
lineObj.Closed = True

أصبح الجزء الثاني كاملاً كما يلي:

Private Sub CalcStar(p() As Double, n As Integer, r1 As Single, r2 As Single)

    Dim lineObj As AcadPolyline
    Dim i As Long, n1 As Integer, ang As Single
    pi = Atn(1) * 4
    n1 = 3 * (2 * n) - 1: ang = 2 * pi / n
    ReDim points(0 To n1) As Double
    For i = 0 To n - 1
        points(i * 6) = r1 * Sin(ang * i) + p(0) 'x
        points(i * 6 + 1) = r1 * Cos(ang * i) + p(1) 'y
        points(i * 6 + 2) = p(2)

        points(i * 6 + 3) = r2 * Sin(ang * i + ang / 2) + p(0) 'x
        points(i * 6 + 4) = r2 * Cos(ang * i + ang / 2) + p(1) 'y
        points(i * 6 + 5) = p(2)
    Next
    Set lineObj = ThisDrawing.ModelSpace.AddPolyline(points)
    lineObj.Closed = True

End Sub

حفظ وتنفيذ البرنامج

قم بحفظ البرنامج، ولتنفيذه انتقل لنافذة أوتوكاد، واكتب الأمر التالي:

vbarun

تظهر نافذة تحوي أسماء الماكروات النشطة، وفي حالتنا يوجد ماكرو واحد فقط، اسمه DrawStar1 ، اختره ثم اضغط الزر Run، ثم أدخل المعطيات في نافذة الأوامر بالترتيب.

أرجو أن أكون قد وفقت في شرح هذا البرنامج البسيط، وآخر دعوانا أن الحمد لله رب العالمين.

تحميل

مشروع VBA