• 
• 
• 

هاتف: +963-31-2220008
جوال: +963-999-824193
سوريا - حمص

مقدمة

سأعرض هنا خوارزمية أخرى في مجال الرياضيات العددية يستخدمها المهندس المبرمج بكثرة في برامجه وهي خوارزمية إيجاد الجذور الحقيقية لتابع مستمر معقد f(x)، أي إيجاد مجموعة قيم x التي تجعل المعادلة f(x)=0 محققة.

سأستعين بكتاب (الرياضيات العددية) للدكتور المهندس سامح جزماتي (منشورات جامعة حلب) لعرض الفكرة ولكن سأعرضها بأسلوبي الخاص ولن أتطرق إلى جميع الطرق المشروحة في الكتاب فالمقصود من هذه المشاركة هو وضع القدم على الطريق، ومن أراد الاستزادة عليه الرجوع إلى الكتاب السابق أو إلى كتب مشابهة.

فكرة عامة

لنفرض أن المطلوب إيجاد جذور التابع:

f(x) = 2 Cos(x) - e^x

أي إيجاد قيم x التي تحقق المعادلة f(x)=0

من الواضح أن المعادلة معقدة ومن الصعب حلها تحليلياً لذلك نلجأ إلى الحل العددي.

قد يكون للمعادلة أكثر من حل (كما في المعادلة السابقة) لذلك نلجأ إلى ما يلي:

1. بما أن الخوارزمية -كما قلنا سابقاً- يجب أن تحوي قيماً ابتدائية فإنه يجب تحديد المجال الذي سيتم البحث عن الجذور ضمنه حتى لا يستمر البحث إلى ما لانهاية، مثلاً نريد البحث عن جذور المعادلة السابقة في المجال [-10,+10]
2. الفصل بين الجذور، أي إيجاد المجالات الموجودة فيها الجذور بحيث يتضمن كل مجال جذراً واحداً فقط، كما في الشكل (2-1) في الأسفل.
3. إيجاد القيم الحقيقية لهذه الجذور بدقة محددة من قبل المهندس، مثلاً بدقة أربعة أرقام بعد الفاصلة.

1 - تحديد المجال المراد البحث ضمنه

هذا المجال يعود إلى خبرة المهندس وإلى طبيعة المسألة والمعادلة.

مثلاً يحدد المهندس البحث من x = -5 إلى x = 5

سنصطلح تسمية نقطة البداية x0 ونقطة النهاية xf وعلى هذا يكون المجال هو [x0,xf]

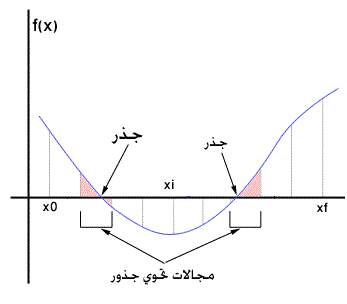
2 - الفصل بين الجذور

في هذه المرحلة يجب البحث عن مجال [x1,x2] بحيث يحوي جذراً حقيقياً واحداً.

نظرية: إذا أخذ التابع المستمر f(x) في ذروتي المجال [a,b] القيمتين f(a),f(b) وكانت هاتان القيمتان بإشارتين مغايرتين أي إذا تحققت المتراجحة f(a).f(b)<0 فإن المجال [a,b] يحوي على الأقل جذراً واحداً للمعادلة f(x)=0 إن كان التابع f مستمراً على المجال [a,b]

جذراً حقيقياً على الأقل فيه

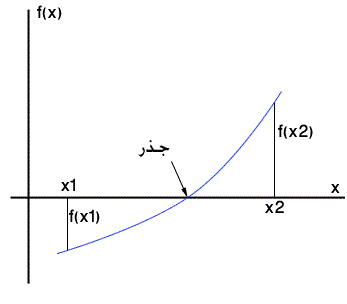
يقوم المهندس بافتراض طول لهذا المجال بحيث يضمن وجود جذر واحد فقط ضمنه أثناء البحث وهذا يتبع لخبرة المهندس وطبيعة المعادلة، وسنصطلح تسمية طول المجال بالرمز dx.

نقسم المجال الأساسي [x0,xf] إلى مجالات صغيرة طول الواحد منها هو dx فنحصل على:

[x0,x1] , [x1,x2] , ... , [xi,x(i+1)] , ... , [...,xf]

حيث:

x1=x0+dx
x2=x1+dx
xi=x(i-1)+dx

ثم نحسب قيمة التابع f في بداية ونهاية كل مجال ونضرب الناتجين معاً:

1. إذا كان ناتج الجداء موجباً فلا يوجد جذر حقيقي، وننتقل للمجال الذي يليه.
2. إما إذا كان سالباً فهذا يعني وجود جذر حقيقي لأن التابع غير إشارته أي أنه تقاطع مع المحور x (على فرض أنه مستمر) لذلك نلجأ إلى إحدى طرق البحث الدقيق عن الجذر ضمن هذا المجال، كما في الفقرة التالية.
   

3 - إيجاد القيم الحقيقية

بعد معرفة المجالات التي تحوي جدوراً نبحث عن القيمة الحقيقية للجذر في كل مجال على حده، وهناك العديد من الطرق (الخوارزميات) لإيجاد هذا الحل منها (المذكورة في الكتاب السابق):

طريقة التنصيف ، طريقة التوسط الداخلي ، طريقة القاطع ، طريقة نيوتون رافسون ، طريقة نيوتون من الدرجة الثانية.

وسأشرح طريقة التنصيف لسهولتها وهي تفي بالمطلوب.

ويجب التنويه أنه على المهندس اعتماد الدقة المطلوبة قبل البدء في الحل ولتكن مثلاً 0.0001 ولنسمها eps

طريقة التنصيف

بعد أن تأكدنا من وجود جذر حقيقي ضمن المجال [xi,x(i+1)] كما سبق فإننا نلجأ لهذه الطريقة للبحث عن هذا الجذر.

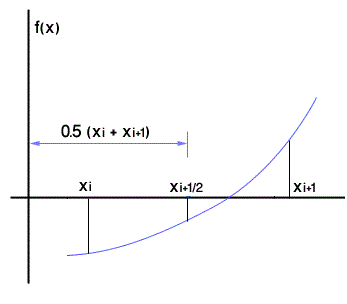
نقوم بتقسيم المجال [xi,x(i+1)] إلى مجالين متساويين هما:

[xi,x(i+1/2)] , [x(i+1/2),x(i+1)]

حيث أن:

x(i+1/2) = (xi + x(i+1))/2

أي أننا قمنا بتنصيف المجال.

ثم نحسب قيمة التابع عند النقطة الوسطية:

إن كانت القيمة المطلقة لقيمة التابع عند هذه النقطة أصغر من eps فإن هذا هو الجذر المطلوب وننتقل للبحث عن جذر آخر في مجال آخر.

أما إن كانت القيمة أكبر من eps فإننا نحدد المجال الذي يحوي الجذر من بين المجالين الجديدين بأن نختبر الجداء التالي:

f(xi) . f(x(i+1/2))

فإن كان الجداء سالباً فإن الجذر يقع ضمن هذا المجال وإلا فإنه يقع في المجال الآخر.

بعد تحديد المجال المطلوب نقوم بتنصيفه مرة أخرى ونحسب قيمة التابع عند نقطة المنتصف وهكذا حتى نحصل على الجذر.

مثال يدوي

هذا المثال منقول من كتاب الرياضيات العددية للدكتور المهندس سامح جزماتي.

المطلوب إيجاد جذور المعادلة:

cos(x) * 2 - e^x = 0

في المجال [0,1] بدقة eps=0.0002

الحل:

1- تحديد المجال الصغير الذي يحوي الجذر:

نعتمد قيمة dx=0.1 للتفتيش عن الجذور ونضع قيم التابع في الجدول التالي:

f(x)	x
1	0.0
0.88484	0.1
0.73873	0.2
0.56081	0.3
0.35030	0.4
0.10644	0.5
-0.17145	0.6

نلاحظ أنه لدينا جذر في المجال [0.5,0.6] لأن إشارة التابع تغيرت.

نلجأ الآن إلى طريقة التنصيف للبحث عن الجذر بدقة.

منتصف المجال [0.5,0.6] هو 0.55:

f(0.55) = -0.02820 > eps

وبما أن f(0.5) = 0.10644 و f(0.6) = -0.17145 فإن الجذر يقع ضمن المجال [0.5 , 0.55] ، نأخذ منتصف هذا المجال : 0.525 فيكون:

f(0.525) = 0.04019 > eps

فالجذر يقع ضمن المجال [0.525 , 0.55] ، نأخذ منتصفه : 0.5375 فيكون:

f(0.5375) = 0.00626 > eps

فالجذر يقع ضمن المجال [0.5375 , 0.55] ، نأخذ منتصفه : 0.54375 فيكون:

f(0.54375) = -0.01090 > eps

فالجذر يقع ضمن المجال [0.5375 , 0.54375] ، نأخذ منتصفه : 0.54063 فيكون:

f(0.54063) = -0.00232 > eps

فالجذر يقع ضمن المجال [0.5375 , 0.54063] ، نأخذ منتصفه : 0.53907 فيكون:

f(0.53907) = 0.00196

فالجذر يقع ضمن المجال [0.53907 , 0.54063] ، نأخذ منتصفه : 0.53985 فيكون:

f(0.53985) = -0.00018

وبما أن القيمة المطلقة للتابع عند 0.53985 أصغر من eps فإننا نعتمد هذا الجذر.

تحويل الطريقة إلى برنامج

قمت بتحويل الخوارزمية السابقة إلى برنامج بلغة فيجيوال بيسيك 6، وهو مرفق مع هذا الدرس، لكن سأنقل نصه هنا لمن لا يستخدم هذه اللغة، ويمكن تحويله بسهولة إلى أي لغة أخرى.

اعتمدت في هذا البرنامج التبسيط ليكون واضحاً لذلك قد يحتاج بعض التطوير.

Public Const e As Double = 2.71828182845905

Public Function GetRoots(x0 As Double, xf As Double, dx As Double, _
                            eps As Double) As Double()
    Dim x1 As Double, x2 As Double, f1 As Double, f2 As Double
    Dim rootsNo As Integer 'The number of roots
    Dim Roots() As Double: ReDim Roots(0)

    x1 = x0: f1 = f(x1)
    For x2 = x0 + dx To xf Step dx
        f2 = f(x2)
        If f1 * f2 <= 0 Then
            'There is a root
            rootsNo = rootsNo + 1
            ReDim Preserve Roots(rootsNo)
            Roots(rootsNo) = BiSectionMethod(x1, x2, eps)
        End If
        x1 = x2: f1 = f2
    Next
    GetRoots = Roots
End Function

Private Function BiSectionMethod(ByVal x1 As Double, _
                     ByVal x2 As Double, eps As Double) As Double
    Dim x0_5 As Double, f0_5 As Double
    Dim Root As Double

    If Abs(f(x1)) <= eps Then
        Root = x1
    ElseIf Abs(f(x2)) <= eps Then
        Root = x2
    Else
        x0_5 = (x1 + x2) / 2
        f0_5 = f(x0_5)
        If Abs(f0_5) <= eps Then
            Root = x0_5
        ElseIf f(x1) * f(x0_5) < 0 Then
            Root = BiSectionMethod(x1, x0_5, eps)
        Else
            Root = BiSectionMethod(x0_5, x2, eps)
        End If
    End If
    BiSectionMethod = Root

End Function

Public Function f(x As Double) As Double
    'f = Cos(x)
    f = 2 * Cos(x) - e ^ x
End Function

هذا البرنامج يتكون من ثلاثة توابع هي:

GetRoots: هو التابع الذي يتم استدعاؤه للبحث عن الجذور، وهو يبحث عن المجالات التي يشك أن فيها جذراً ثم يطلب من التابع BiSectionMethod أن يجد له هذا الجذر، ومن الممكن أن يطلب من تابع آخر أن يجد له هذا الجذر كما أشرت أعلاه.

BiSectionMethod: هو التابع الذي يستخدم طريقة التنصيف على مجال محدد.

f: وهو التابع الذي نبحث عن جذوره، وقد فصلته في برنامج فرعي مستقل لتسهيل الوصول إليه وتغييره.

الآن لاستدعاء التابع الأول نطلبه بأي أسلوب مناسب، فمثلاً، نضع زراً اسمه cmdSolve على نافذة، ونضيف أدوات نصوص نكتب ضمنها حدود المجال والدقة، ثم نكتب ضمن الحدث Click للزر السابق ما يلي:

Private Sub cmdSolve_Click()
    Dim Solution() As Double, i As Integer
    Solution = GetRoots(Val(txtX0.Text), Val(txtXf.Text), _
                Val(txtDx.Text), Val(txtEps.Text))

    lstSolution.Clear

    If UBound(Solution) > 0 Then
        For i = 1 To UBound(Solution)
            lstSolution.AddItem Solution(i)
        Next
    Else
        lstSolution.AddItem "(no roots)"
    End If
End Sub

ملاحظة: أسماء مربعات النص تبدأ ب txt ومابعد هذه الكلمة يدل على وظيفتها.

تحميل

• البرنامج السابق بلغة VB6.